凡人皆需数学

欢迎来到梦开始的地方。此前的章节概述了“什么是伪教育”、“贯穿本科的唯一主线：知行”。本章（数学）和下一章（马克思主义哲学）将提纲挈领地介绍“见天地”的主要矛盾：数学和哲学。为什么本文是梦开始的地方？详细答案参见“下篇：自我教育/0x07 信息素养”。在此，长话短说版：“听过很多道理，依然过不好这一生”是平庸的人甚至伟大的人的通病。但是，可以让你过好未来几百年的数学和哲学覆盖你的一生简直绰绰有余。之所以它们是在知行皇冠上的两颗明珠，是因为相比于数学和哲学的皓月之辉，以萤火之光称呼你所听过的很多道理都已经极大地过誉了。从“听过很多道理”的层面，数学将告诉你：自然语言是错漏百出的屁话；从“依然过不好这一生”的层面，哲学将告诉你：人生之宏大，远远不在于“过好这一生”这种毫无难度可言的小目标。

0x01 引例：最高年薪

1. 建模

自然语言：A是上海脚痛大学计算机科学与工程系研一的在读硕士。根据上一届学长学姐的就业数据以及个人在同侪之间的相对实力，ta确定了自己挣钱小目标：最高年薪的下限是300,000￥，上限是900,000￥，最可能是500,000￥。糟糕，A成“行走的50w”了！

数学语言：

• 绝大多数普通人服从“work-life模型”。将work映射为挣钱。
• 为了简化，将目标函数设置为最高年薪（单位：万元）。
• 考虑到各种随机因素，最高年薪在某个区间内上下浮动。因此，定义二元组 $D=\left\{\left[min,max\right],mle\right\}$ ，其中， $\left[min,max\right]$ 代表最坏情况与最好情况所对应的年薪区间（区间估计）； $mle$ 代表最可能情况所对应的年薪点（点估计）。为了直观，将二元组 $D_0$ 赋为具体的值。
• 不妨假设上海脚痛大学计算机科学与工程系应届硕士的最高年薪 $S$ 服从正态分布 $N\left(60,10^2\right)$ 。
• 基于 $3\sigma$ 原则，将 $\left[min,max\right]$ 设置为 $\left[\mu -3\sigma ,\mu +3\sigma \right]$ ，即 $\left[30,90\right]$ 。
• 之所以将 $mle$ 设置为 $50$ ，是因为A在同届硕士中的分位点 $\alpha$ 映射至正态分布 $N\left(60,10^2\right)$ 的横坐标为 $50$ 。
• 综上，初始的最高年薪二元组 $D_0=\left\{\left[30,90\right],50\right\}$ 。

2. 误差

自然语言：由于每届的生源质量、就业环境等因素不同，A考虑此差异对挣钱小目标的影响。ta将上一届和自身水平相似的学长作为参考对象，以二人的外部客观条件（学历的含金量、实验室的业内知名度、导师的人脉资源等）、个人主观条件（内卷程度、学习能力、表达能力等）和就业环境差异（经济形势、行业兴衰等）作为修正挣钱小目标的依据。经此修正，ta的挣钱小目标变成了：最高年薪的下限是200,000￥，上限是800,000￥，最可能是400,000￥。嘿嘿，A又不是“行走的50w”了！

数学语言：

• 考虑到每届的差异，有必要根据自我奋斗和历史进程修正 $D_0$ 。
• 不妨假设矩阵 $A$ 代表外部客观条件（学历的含金量、实验室的业内知名度、导师的人脉资源等），向量 $x$ 代表个人主观条件（内卷程度、学习能力、表达能力等），向量 $b$ 代表offer（初始年薪、最高年薪、工作强度等）。设向量 $b$ 的第 $k$ 个元素 $b_k$ 为最高年薪。
• 已知上届同分位点的学长满足 $Cx=d$ ，A满足 $Ey=f$ 。设修正因子 $\Delta D=f\left(C,E,x,y,\delta \right)$ ，其中， $\delta$ 代表由经济形势、行业兴衰等因素所造成的就业环境差异。
• 设修正三元组 $\Delta D=\left\{d_{min},d_{max},d_{mle}\right\}$ ，不妨令 $\Delta D=\left\{-10,-10,-10\right\}$ 。
• 综上，经过修正的最高年薪二元组 $D_0=\left\{\left[20,80\right],40\right\}$ 。

3. 决策

自然语言：A在软件开发工程师和程序分析研究员两个岗位之中纠结：前者的成功率更高，但待遇更低；后者反之。根据薪资分布、主观条件（对技能树的偏好、学习基础等）、客观条件（实验室资源、学习难度等），ta量化了二者的成功率和最高年薪，选择了数学期望更大的程序分析研究员。

数学语言：

• 设个人综合实力所对应的最高年薪为 ${\beta }_k$ ，工作所对应的最高年薪为 ${\gamma }_k$ ，工作的获取概率 $p=g\left({\beta }_k,{\gamma }_k\right),p\in \left[0,1\right]$ 。
• 记获取概率向量 $P={\left(p_1,p_2,\dots ,p_n\right)}^T$ ， $p_k$ 代表第 $k$ 种工作的获取概率；记最高年薪向量 $\gamma ={\left({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\right)}^T$ ， ${\gamma }_k$ 代表第 $k$ 种工作的最高年薪。
• 为了数学期望最大化，A所选定的工作满足 $p_t\cdot {\gamma }_t=max\left(p_i\cdot {\gamma }_i\right),i\in \left\{1,2,\dots ,n\right\}$ 。为了简化，设offer所构成的集合为 $\left\{A,B\right\}$ ，其中，获取概率 $\left({\alpha }_A,{\alpha }_B\right)=\left(0.8,0.75\right)$ ；最高年薪 $\left({\gamma }_A,{\gamma }_B\right)=\left(45,50\right)$ 。
• 工作 $A$ 最高年薪的数学期望是 $0.8\times 45=36$ ；工作 $B$ 最高年薪的数学期望是 $0.75\times 50=37.5$ 。因此，A将工作 $B$ 所对应的技能树 $T_B$ 作为学习目标。
• 综上，A以最高年薪的数学期望为 $37.5$ 的工作 $B$ 为目标，学习其技能树 $T_B$ 。

4. 计划

自然语言：A按照程序分析研究员的招聘要求确定了第1年、第2年和第3年的学习目标；年初时，ta将该年的学习目标划分为每月的学习小目标；月初时，ta将该月的学习小目标划分为1h左右的学习任务；周日时，ta选取若干学习任务作为每周学习计划；最后，ta将每周学习计划的学习任务分配至各个工作日。

数学语言：

• 在技能树 $T_B$ 的学习过程中，A的实力 $I_B$ 逐渐提高。显然， $I_B$ 是关于时间 $t$ 的函数。
• 定义打工人集合 $\Phi =\left\{{\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n\right\}$ ，且 ${\varphi }_M$ 为该集合的“广义众数”。
• 设 $I_B^{\prime }(t)=h\left({\varphi }_M,t\right)$ ，其中， $h\left({\varphi }_M,t\right)$ 是面向工作 $B$ 所需技能树的一般化学习曲线。
• 为了便于分配学习任务并及时地获得正反馈，将总区间 $\left[t_0,t_0+\Delta t\right)$ 依“年、月、周、日、时”划分为若干子区间。不妨设 $t_0=0$ ， $\Delta t=2.5$ （单位：年）。

5. 迭代

自然语言：每天早晨，A确定当天的学习任务；根据当天的学习反馈，ta总结学习任务的合理性以提升计划能力、总结学习任务的执行情况以提升执行能力。随着学习的深入，A的总结能力也不断提升。

数学语言：

• 将学习周期分为三个阶段：计划、执行和总结，即 $\left(P,E,S\right)$ 。
• 为了简化，暂时固定执行 $E$ 和总结 $S$ 。
• 执行 $E$ 和总结 $S$ 不断地产出后验信息，该后验信息可以用于优化计划 $P$ 。因此，不妨以天为单位，将 $p^{(i)}$ 定义为第 $i$ 天的计划能力。
• $\exists k>0$ ， $\forall N>k$ ，使得 $\left|p^{(N)}-p\right|<ϵ$ ，即： $p^{(n)}$ 收敛于 $p$ 。
• 执行能力 $e$ 和总结能力 $s$ 亦同。

6. 下一个目标

自然语言：在两年半的练习时长之后，A海投简历。经过层层筛选，ta获得了最高年薪分别为230,000￥、260,000￥、330,000￥和420,000￥的一众offer，并选择了420,000￥的offer。ta通过这次挣钱小目标的实践更新认知体系，启动了下一个目标。

数学语言：

• 两年半的练习时长已到，A的实力达到了 $X_B$ ，而且向 $X_B\pm 3{\sigma }_B$ 的所有岗位投递了简历。
• 经过层层筛选，A收到了 $m$ 个offer。
• 对于offer所构成的集合 $O=\left\{o_1,o_2,\dots ,o_m\right\}$ ，A选择了 $o_{max}=max\left\{o_i\right\},i\in \left\{1,2,\dots ,m\right\}$ 。不妨设 $O=\left\{23,26,33,42\right\}$ ，则 $o_{max}=42$ 。
• A分析了以挣钱小目标——最高年薪为导向的初态 $state\left(t_0\right)$ 、实践的过程 $p\left(T_B\right)$ 、终态 $state\left(t_0+\Delta t\right)$ ，将这次实践所产出的后验认知加入认知体系，启动了下一个目标。

0x02 分类讨论

我相信绝大部分小镇做题人对初等数学、数学，乃至哲学不感兴趣。那么，本文和本章的引例告诉你：“上街买菜不需要微积分，但你确实需要微积分。”

我的数学水平仅限于初等数学的“大致粗通、局部精通”和高等数学的“大致粗通、局部的局部精通”。我以自己为界：如果你的数学水平足以向下兼容我，那么你应该足以触碰最艰深的数学，因为我足以触碰最艰深的数学；如果你的数学水平不足以读懂本章，那么你的人生大概率也可以被一眼望穿了，因为本章所涉及的数学仅仅是理工科高级知识分子的常识。在上下求索的四年里，数学和哲学将是、也应该是你们最难的噩梦，但将成为、也应该成为你们披荆斩棘的利刃。

数学将广大埋头内卷的做题人分成了三类：

• 小镇错题本：这个群体是应试数学的受害者。ta们由于各种千奇百怪的原因，或早或晚地离开了初等数学。就我所知，对于大部分师资水平一般的地区或学校而言，“数学越好的人天赋越高”这一观点甚嚣尘上，但事实并非如此。数理逻辑越强的学科，学生一旦掉队，几乎无法跟上滚滚向前的升学。教育水平较低的“小镇”，没有人为你的数学保驾护航。于是，数学使得做题人早早地两极分化：越会做题的人越喜欢做题；越不会做题的人越不喜欢做题。但是，准大一的你们完全有机会重拾数学，也完全有能力重拾数学。
• 小镇做题家：被称为小镇做题家的人往往得到了初等数学的眷顾，有了学习高等数学的机会，但你们将成为高等教育的受害者。写得和屎一样的教材以及宽松的学习环境，使得一部分小镇做题家以“我上街买菜还需要二重积分吗”为自己学不好高等数学或懒惰找借口，而另一部分小镇做题家抄应试初等数学的作业，轻而易举地在有手就行的考试中拿到高分，但对高等数学毫无理解。
• 普信做题家：数学和普信有什么关系？碍于家族的积累，小镇做题家在本科期间完全是背景板，是为普通；数学的数理逻辑能力附带了自信。如果你可以彻底地理解本章，你必将普通且自信。

如果你认为你的数学水平非常低，抽空重学一遍初等数学。哪怕翘了大一所有的高等数学课，也必须重学一遍初等数学。否则，即使本书除了本章之外几乎没有数学符号，你对本书的吸收度也会特别差。

0x03 应用场景

之所以选择“最高年薪”这个引例，不仅是因为大家都关心挣钱，而且是因为它串起了若干高等数学的定义（第1节加粗的文字）和数学思想的应用。相反地，一旦你掌握了高等数学，比如理解了定义或数学思想，应用场景可谓信手拈来。

1. 网上冲浪的自我修养

遇到自以为是的键盘侠，不要和它对喷，直接甩它三个题目：

(1) 存在一台机器，按左键，75%的概率掉落100元；按右键，必掉落70元。每位玩家拥有10000次按键机会，你将如何分配按左右键的比例？

(2) 小陈每天打5h乒乓球，ta更有可能是（）。

A：小学数学老师

B：热爱乒乓球的小学数学老师

(3)【三门问题】参赛者面对三扇关闭的门，其中一扇门的后面是一辆汽车，选中了可赢得该汽车；另外两扇门后面各是一只山羊。当参赛者选择了一扇门，但未开启它。此时，节目主持人开启后面是山羊的一扇门，并询问参赛者要不要换成另一扇仍然关闭的门。换另一扇门是否增加参赛者赢得汽车的机率？

最后，把喷子拉黑就行了。

2. 正态分布

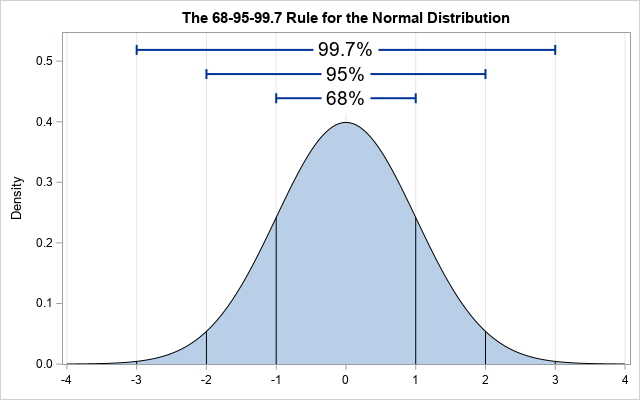
横坐标可以是任何人事物。例如：

• 为每件事情的善良度打分，无善无恶为 $0$ 分，极善为 $4$ 分，极恶为 $-4$ 分。你每天在现实中经历的事情和在互联网上看到的事情，善恶度的差异是不是很大呢？如果一个人通过传播负能量极强的简体中文互联网认识世界，那ta的三观会受到怎么样的影响呢？
• 为网友的言论打分，无感为 $0$ 分，无比认同为 $4$ 分，无比反对为 $-4$ 分。你刷不刷App的推荐呢？你的偏好和点赞是否影响了推荐？如果一个人主要通过App的推荐摄入信息，那ta的认知会受到怎么样的影响呢？

3. 粗糙の决策模型

存在一台机器，按左键，75%的概率掉落100元；按右键，必掉落70元。每位玩家拥有10000次按键机会，你将如何分配按左右键的比例？

人生也是这样一台机器，只不过按键和数字不一样而已。如果掌握了概率论与数理统计，你就不会一直在人生的岔路口处精准地作出错误的选择了。

4. 粗糙の旁观者模型

以高考填志愿为例：

• Aのb专业 vs Bのd专业

• Fのt专业 vs Yのo专业

• 当局者：下面一堆笨比信誓旦旦地回答“选Aのb！选Bのd！选Fのt！选Yのo！因为我怎么怎么样、我认识的谁谁谁怎么样。”

• 旁观者：如果先基于ta们字里行间的bias修正ta们所呈现的instance，然后将所有已修正的instance拟合成概率分布，再根据个人情况确定自己在该分布中所处的位置，会不会比“挑一个或挑一些回答作为参考”更好呢？

因为“当局者迷，旁观者清”。

5. 终身学习

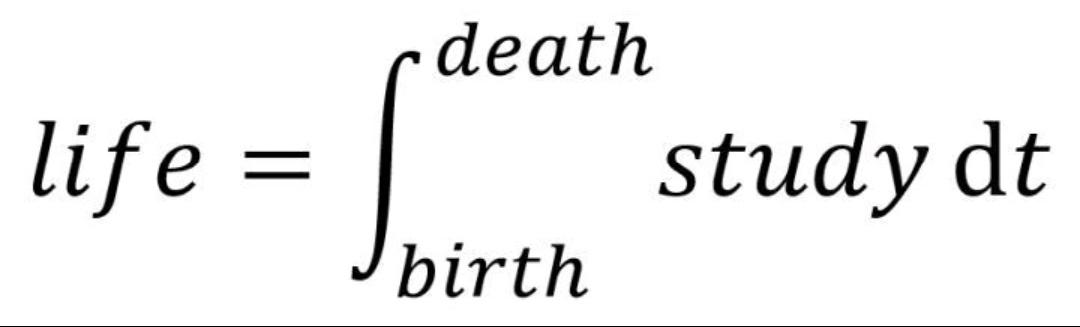
6. 学习曲线

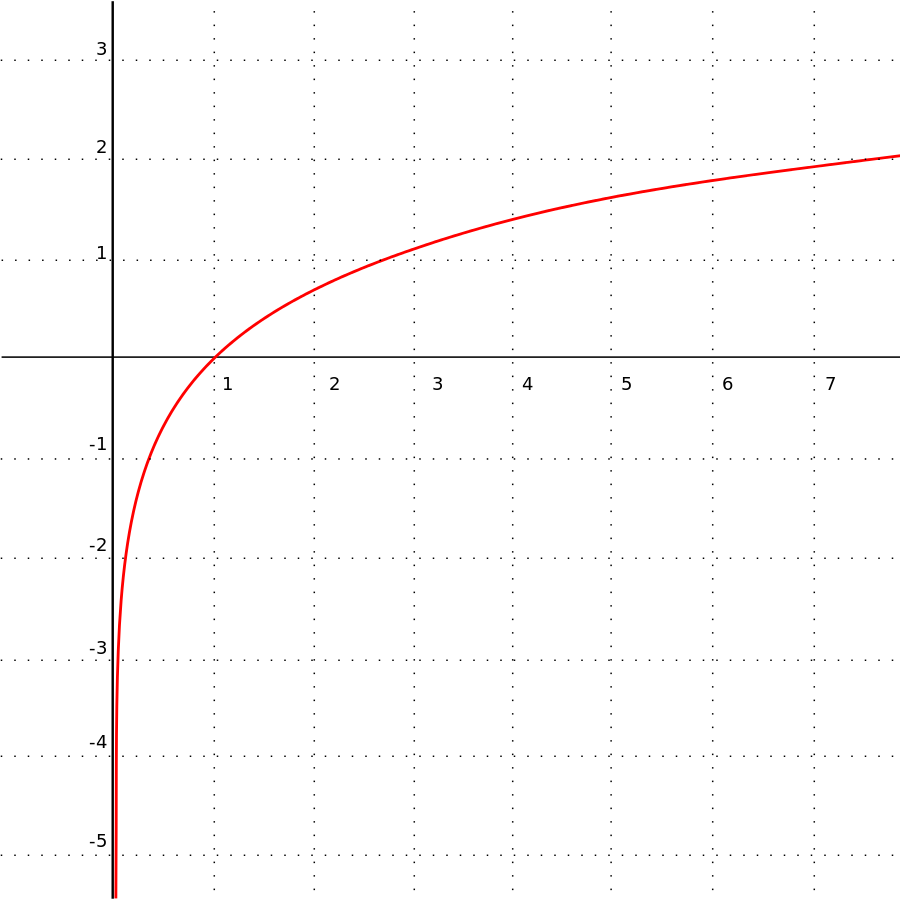
• 如果理解了学习曲线往往是对数型的，你是否还会为起步晚而焦虑呢？
• 如果理解了沿着梯度的方向增长最快，你是否还会执着于“每日一题”的日积月累呢？
• 如果理解了多元函数，进而定义了自己的“人生函数”（某些自变量，非你莫属、非你莫有），你是否还会对曾经那条千军万马过独木桥的、单向度的赛道心存执念呢？

凡人不会因为需要数学而伟大，但会因为不需要数学而平庸。