目标模型

0x01 引例：时间管理

1. 目标 to 任务

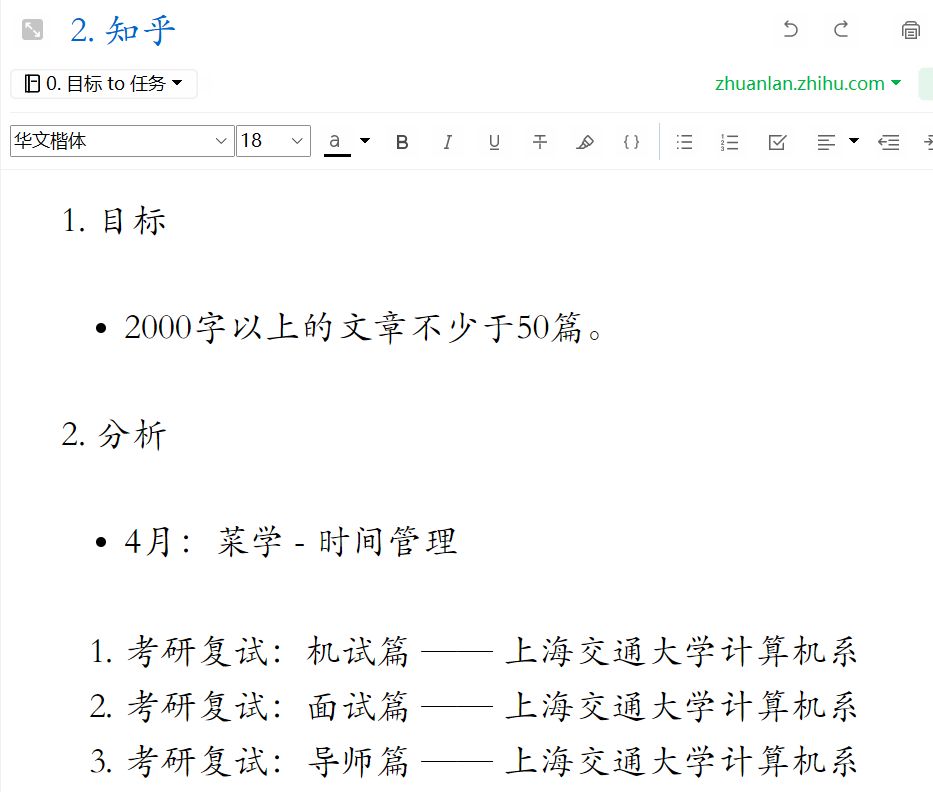
我的日记本以年为单位。首先，我每年会设立一些目标，时间跨度在半年到一年之间。在设立目标之后，将每个目标分解为一系列可直接执行的任务，任务的执行时间从0.5h到1h不等。随着实践的深入，不断地调整目标和任务。等到所有任务完成了，目标也就实现了。

以写知乎为例，我之前每周六晚上花3h写2000字左右。 $50\times 7=350$ ，笔耕不辍方可实现。

2. To Do List

日记的第1部分是To Do List。你可以把所有已确定deadline的任务放在这里，一来，作为备忘录；二来，适当地给自己一些压力；三来，将已完成的任务从To Do List中移除可以带来正反馈和成就感。有一个不得不提的小建议：写好模板。在To Do List新增任务的时候，在模板里添加；在完成任务之后，在模板里删除。理想的状态是“每天起床，复制模板；从To Do List中选择任务，填满整块时间；执行，在完成任务后将其从模板中删除；每天的碎片时间或每周特定的整块时间，补充To Do List。

3. 记录

日记的第2部分是“计划＋记录”。从To Do List中选取任务是为计划；记录实际的执行情况（<n/m>：m表示任务的计划时长为m小时；n表示任务的已执行时长为n小时）。

4. 日省吾身

日省吾身是“谋一日以谋一生”的核心所在。第一，我只跟自己卷，别人强不强可以影响我的判断，但绝对不影响我的心态。第二，进步 = 时间 × 效率，而实力和进步（自变量）的函数关系近似于对数函数，通过自律和高效成为优秀的人只是时间问题。

• 健康管理：身体是享受生活的本钱。有命活，才有命体验。
• 时间管理：优化效率，反思计划的执行情况。必须思考的问题是，如果重新开始，如何度过今天？
• 社交管理：优化社交。反思人事物的交互。同上。如果重新开始，如何改进社交？

当然，每个人可以根据自身的价值观，选择三省吾身的主题。每天的自省一定会发现某些优化点反复出现。将该优化点设置为一个习惯。从0开始计数，做到加1，没做到归零。若每月做到了21天，基本养成了一个新的好习惯。

5. 涓滴体验

每天花一些时间做自己喜欢的事情，这是时间管理的意义所在。涓滴体验可以源于爱好，也可以源于意料之外的小确幸，还可以是发自内心的悲伤和喜悦。如果说其它时间是为了谋生，那么涓滴体验就是为了生活。以后重温来时路，这个部分将会成为赛博时间囊。

6. 总结

所谓的总结（图中未显示的第3部分），即复盘。无论目标成功或失败，分析结果可以纠正自己错误的认知。总结的本质在于提高“做成一件事”的能力。把任何目标都当作相同的一件事，目标 $\to$ 分析 $\to$ 总结。久而久之，你终将求仁得仁。

0x02 可行性分析

和本节关系最密切的课程是《线性代数》。正常的工科生对《线性代数》的主要需求是让向量化、矩阵化的数据可以充分地挖掘计算机的算力。平凡之路将其用于目标的可行性分析。

1. 线性方程组

先通过几个线性方程组让数学和目标的可行性挂钩：

$$\{\begin{array}{l}x+y=9\\ x-y=1\end{array}$$

正定：方程存在唯一解。

$$\{\begin{array}{l}x+y+z=9\\ x-y-2z=1\end{array}$$

欠定：方程存在无穷多解。

$$\{\begin{array}{l}x+y=9\\ x-y=12\\ x+3y=4\end{array}$$

超定：方程无解。

2. 定

从上帝视角来看，世界可能是正定的；从个人视角来看，世界必然是欠定的。换言之，你无法为任意足够小的目标建立正定的数学模型。在本小节中，你需要理解和正定、欠定、超定相对应的三个模型：决定论、概率论和混沌论。

A. 决定论

假设时空的起点是宇宙大爆炸、时间是量子化的、世界是正定的，那么现在和未来早已注定。因为没有相关的物理背景与哲学背景，所以我不过多分析，以免暴露本人粗浅的学识。对决定论感兴趣的读者，可以自行了解和思考。注意，决定论和宿命论完全不同。决定论是具有物理背景的哲学概念；虽然宿命论似乎也沾点哲学，但它和宗教、文化的关系更大。

你信仰投骰子的上帝；我却信仰完备的定律和秩序。

——爱因斯坦

本文的决定论模型：所有的人事物存在某个起点。假如拿到了该起点的所有信息，我们可以精确地推演未来的任意时刻（唯一解）。

至少迄今为止，我的每一个重大的目标、每一个重大的决策、每一个重大的错误，都可以找到相应的过去。决定论所管辖的范围至少包括“马后炮的自洽”。你应该让所见所闻被自己的认知体系合理化。

一言以蔽之，决定论解释过去。

B. 概率论

如前文所说，从上帝视角来看，世界可能是正定的；从个人视角来看，世界必然是欠定的。假如我们把 $A$ 砍掉几行（漏掉了几行信息，欠定了）。此时，解的形式为 $x=x_0+k_1\cdot x_1+k_2\cdot x_2+...+k_n\cdot x_n$ 。为了简单起见，我们不考虑线性组合所导致的无穷多解，而是简化为“线性方程组的解可能是 $x_1$ 或 $x_2$ ，而且是 $x_1$ 的概率为 $p_1$ 、是 $x_2$ 的概率为 $p_2$ ，而且 $p_1+p_2=1$。”

在人生的岔路口，我们经常面临类似的情境，比如“考研清华大学，成功率30%，收益100”、“考研厦门大学，成功率70%，收益70”、“考研南昌大学，成功率98%，收益10”。假如采用《下篇：自我教育/2 数学/3 人生模型》的贪心算法，不考虑在考研成功之后的状态（多阶段的动态规划），可以算出各个选择的收益：“厦门大学49 > 清华大学30 > 南昌大学9.8。”厦门大学49、清华大学30、南昌大学9.8的量化思维正是数学的优势所在。

本文的概率论模型：所有的人事物存在某个起点。假如拿到了该起点的所有信息，我们可以推演未来的任意时刻（唯一解）。但是，我们必然拿不到该起点的所有信息。通过欠定信息，我们可以预测未来的若干可能选项（及其收益和概率）。

这个模型又可以负责你人生的哪些部分？其中之一是力所能及地作出最优的决策而且无悔。后者是一种相当稀缺的品质。

一言以蔽之，概率论决定现在。

C. 混沌论

Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities.

理工科学生可能有一门必修课，大学物理实验。我当年的大学物理实验似乎有一节课的教学内容是看视频。那个视频演示了什么是混沌（物理意义）。这填补了我的空白：“有了积跬步至千里的微积分（决定论）、量化不确定性的概率论与数理统计（概率论），再加上让人放弃治疗的混沌（混沌论），岂不是足以合理化一切吗？”如果不从物理学中了解混沌，你可以使用“蝴蝶效应”替代之。

The flap of a butterfly's wings in Brazil set off a tornado in Texas.

——Edward N. Lorenz

个人在自然、社会、历史中的能力顶破天，也就是顺应大潮了。从某种程度上来说，人类已经把人类文明养成了一个庞然巨物。经由长期的自我教育，你才勉强均匀地了解它。在未涉足的领域，不断地爆发着你无法预料的新知。混沌论告诉我们，守好分内寸土即可。

在2023-04-30的10:00左右，我在白金汉爵大酒店第12层的某个房间里，透过（近）落地窗俯瞰下面的街景，惊喜地发现了我在初到上海的时候所住的魔方9号楼。远在2021-06，我对科研有着绝对的纯粹。老板放不放实习？无所谓！科研失败以致于把号练废了？无所谓！因为没有科研基础，我踩遍了科研所有的坑。对同学“找老婆比搞科研更重要”的贯耳魔音，我不屑一顾。在半个月之后，我认识了一个女生、谈甜甜的恋爱、谈苦苦的恋爱。咚！咚！咚！四月之声。爱灰飞烟灭。在进上海交通大学之前，我要写一手好代码；2022年，聆听中华大地此起彼伏的悲鸣……疫情、小行星撞地球，这是大的混沌；又一个明星塌房了、又一个博士自杀了，这是小的混沌。如果知道自己能力的边界在哪（“见自己”的必要条件），则在边界之外的世界均为混沌。

一言以蔽之，混沌论放弃未来。

注意，“混沌论放弃未来”与消极没有关系，因为你只需要通过决定论和概率论决定现在，就决定了自己的绝大部分未来。混沌论所放弃的未来是未知的未来。其放弃是一种减少精神内耗（不切实际的完美主义）的放弃，而不是自暴自弃。

3. 现实意义

方程存在唯一解、方程存在无穷多解、方程无解是数学意义。那么，多元一次方程组映射至平凡之路的现实意义是什么呢？

和《下篇：自我教育/2 数学/1 凡人皆需数学》类似：

$$Ax=b$$

矩阵 $A$ 表示目标的背景情况（比如条件、约束、个人基础）；向量 $x$ 表示解决方案；向量 $b$ 表示目标。

继续结合前文《下篇：自我教育/2 数学/3 人生模型》，正定对应求而得、欠定对应不求而得、超定对应求而不得。

建立数学模型往往是难的，但你不需要把每个目标析构一遍。在学习数学的过程中，你将在数域的扩充中潜移默化地感受数学整套形式化框架的搭建、“在难题中潜移默化地感受以比较长的因果链解决朴素、简洁、和人生意义八竿子打不着的难题”、数学思想将自然而然地成为独立思考的利器。就“正定”而言，它告诉你：“假如你清晰地认识了目标的背景情况 $A$ 、清晰地给出了解决方案 $x$ ，那么结局 $b$ 已经注定了。”或者反其道而用之，假如你清晰地认识了目标的背景情况 $A$ 、清晰地给出了合理的目标 $b$ ，那么你所需要做的事情有且仅有“相信自己只要将合理的解决方案执行到位，成功水到渠成”。或者马后炮地说，假如你失败了，把 $Ax=b$ 玩成了 $Cy=d$ ，你可以修正你的认知体系，从 $Ax=b$ 重定向至 $Cy=d$ 。

我们可以从“定”出发，看看不经自我教育洗礼的国产大一新生如何犯错：

• 沉迷奶头乐。在一个制作国民级手游的团队里，有多少心理学博士？任何土生土长的做题人，在一考定终身、学而优则仕的持续洗脑下，不可能没有尝试过逆袭。引用一个大家更加熟悉的表达“间歇性踌躇满志；持续性混吃等死”。暂且不说别人，单单我自己便在半年前才注销了王者荣耀的账号。不妨将“踌躇满志”作为目标 $b$ 的一部分，我们看不到“持续性踌躇满志”需要与一堆北京师范大学心理学博士为敌。也就是说，在沉迷奶头乐的土生土长做题人眼中， $Ax=b$ 的 $A$ 与北京师范大学心理学博士毫无关联。按照上文的“假如你失败了，把 $Ax=b$ 玩成了 $Cy=d$ ，你可以修正你的认知体系，从 $Ax=b$ 重定向至 $Cy=d$ ”， $C$ 至少多一维“北京师范大学心理学博士的PUA”；相应的 $d$ 至少多一维“防止北京师范大学心理学博士的PUA”。这未必可以解决“持续性混吃等死”这一问题，但至少提供了解决它的可能性。随着你的认知水平越来越高， $Ax=b\to Cy=d\to Ez=f\to ...$ ，成功也近在咫尺了。
• 只见树叶，不见树。标准的国产大一新生可能有一个学习收藏夹（比如知乎、哔哩哔哩、小红书），里面放了很多学习资料。它们可能是清北做题家分享的应试技巧、可能是双非黑马逆袭的考研经验贴、可能是知识区博主的书单和万字解析。为什么我猜得这么熟练啊！？不妨将《下篇：自我教育/2 数学/3 人生模型》最宏大的目标函数“度过幸福的一生”作为 $Ax=b$ 的 $b$ 。在服务于此目标的 $A$ 中，至少有一些矩阵元素属于学习资料（即学习收藏夹所存放的内容）。暂且忽略“放进收藏夹吃灰”的行为艺术，它们足不足以纳入矩阵 $A$ 呢？答案是否定的。假如 $b$ 仅仅对应考上985、考研上岸、每年读10本书这种目标，将App收藏夹的学习资料作为 $A$ 的元素是OK的，但对于“度过幸福的一生”，这些从全知之树飘落的信息碎片便不足够了。换言之，你的信息素养无法为自己的目标 $b$ 提供一个适配的矩阵 $A$ ，使之辅以可行的解决方案 $x$ 达成目标。
• 无法大事化小，小事化无。假设已经建立了某个目标的正定模型，即目标的背景情况被映射至 $A$ ，目标被映射至 $b$ ，且 $Ax=b$ 存在唯一解。你会解 $x$ 吗？在前面所举的例子（二元一次方程组）中，矩阵和向量的维度是很小的，所以你可以通过“消元法”，甚至一眼看出 $x=5,y=4$ 。但是，当矩阵 $A$ 是 $5\times 4$ 的规模，你应该就需要诸如 $[Ab]\to [Ex]$ 的解法了；当矩阵 $A$ 是 $5000\times 4000$ 的规模，你应该只能通过计算机求解了。线性方程组的“消元法 → 初等变换法 → 编程法”的升级，其最自然、最高效、收敛性最强的打开方式正是“学习数学”，而“度过幸福的一生”的“消元法 → 初等变换法 → 编程法”的升级，自然、高效、具有收敛性的打开方式之一是“见天地”、“见众生”、“见自己”。

照应前文，任何平凡的生活方式均存在完整的复刻路径；任何伟大的生活方式均不可能通过路径依赖实现。平凡之路反反复复地出现。它的充分条件反反复复地出现；它的必要条件反反复复地出现；它的充要条件反反复复地出现。本文再出现一次。结合68–95–99.7 rule，我们可以将在概率论中发生概率不低于95%的事件近似地纳入决定论的范畴，比如上文所提到的“考研南昌大学，成功率98%”。只要你的 $Ax=b$ 模型近似正确，该事件近似为必然事件。精通正定的决定论、欠定的概率论、超定的混沌论，在68–95–99.7 rule之下，是平凡之路的充分条件，也是伟大之路的必要条件。平庸的人不懂得控制欲望，以致于矩阵 $A$ 的秩自发地猛涨。

假设矩阵 $A$ 的秩是 $m$ 、向量 $x$ 的维度是 $n$ ，当 $m=n$ 时，关于目标 $b$ 的线性方程组是正定的。理性缺缺的人类，一旦实现了一两个小目标，秩往往涨三四个维度，所以永远无法满足膨胀的欲望。或者，平庸的人习惯于阉割目标 $b$ ，从而减秩。从方法论的层面来看，超定之苦的解决之道分为开源和节流。

• 开源：增加向量 $x$ 的维度 $n$ （解决方案的“穷则变、变则通、通则久”）。
• 节流：降低矩阵 $A$ 的秩 $m$ （注意，只是降秩，而不是减少矩阵的行数，否则阉割了目标 $b$ ）。

当 $n$ 略大于 $m$ 时，目标具有比较高的可行性。

• “大于”即存在解。
• “略”保证了 $x=x_0+k_1\cdot x_1+k_2\cdot x_2+...+k_n\cdot x_n$ 的 $n$ 不会太大。

0x03 决策

本节的理论依据是《概率论与数理统计》。最核心的知识点仍然是《随机漫步的傻瓜：极简概率论》和《下篇：自我教育/2 数学/1 凡人皆需数学》的数学期望。

其它内容（最大似然估计、均值回归等）暂时不展开。

0x04 计划

对于给定的目标，计划包括三要素：现状、目标和策略。

1. 现状

以高考为例：

• 见自己（主观）：硬实力和软实力。
  • 硬实力：（语文）写作水平如何？记忆力怎么样？（数学）小学数学学得怎么样？初中数学学得怎么样？（英语）词汇量？听说读写？
  • 软实力：应试体系什么水平？认知能力？信息素养？情绪管理？执行力（自律）？
• 见天地（客观）：外力和阻力。
  • 外力：教辅资源？是否有做题家的兄弟姐妹？
  • 阻力：高中笨比老师的数量？寝室环境和室友？
• 见众生（随机性）：人事物。
  • 人：数学大小年？
  • 事：新冠突发？试卷被龙卷风刮跑了？临考生病了？
  • 物：考场的文具不好用？考试桌椅晃？空调的温度不合适？

为什么说高考（考试）相对简单呢？但凡把考研换成别的事情，带来随机性的人事物就完全不一样了。

• 人：傻逼领导；空降的关系户；被Donald Trump或Joe Biden制裁。
• 事：新冠突发；亲人生病。
• 物：笔记本突然死机；U盘坏了；闹钟没响！

2. 目标

清晰。烂的目标：考入上交计算机系；好的目标：高考675+分。低分或高分被录取、大小年，这些不清晰的元素使得“考入上交计算机系”对应的状态非常模糊。

实际。烂的目标：备考时间1个月，考入清华计算机系；好的目标：裸考分数是多少？分数增长曲线是什么？有效备考时间是多少？目标分数是多少？需要强调的是，如果明确地知道一个目标的成功率是20%，而且愿意接受80%的失败风险，那么它仍然是很实际的目标。对成功率的估计和实际成功率越接近，目标越实际。

可变。常立志是立长志的前提。有一句老话，“无志者常立志，有志者立长志”。但是，没有人可以早早地在不知行的情况下树立终身行之的人生目标。好的目标必须经得起修改，也只有不断的修改，才能确定“求仁得仁”的“仁”。良性的修改：修改的幅度越来越小，直至稳定。

3. 策略

车到山前必有路，船到桥头自然直。策略由现状和目标决定，存在可执行方案是常态。此外，可以放弃目标。失败而已，没什么大不了。不要妄自菲薄；不要沉浸在焦虑等负面情绪中；不要在不理智的时候作出影响人生进程的重大抉择。

图式。这是一个心理学概念，将其替换成维度或许更合适。思考问题的维度越高，备选策略越丰富。图式越复杂，认知水平越高，策略越多，且剪枝能力越强。以高考数学为例，如果只在初等数学里折腾，高考那道压轴题永远会是一道坎，但如果某些人已经提前学完了微积分呢？降维打击。

0x05 成败

1. 悖论

上文的最后一节也解构成败。本小节顺着《线性代数》“定”的视角继续解构决策的成败。

一个决策正确与否取决于每个人对正误的定义；而决策的数量则取决于每个人对决策的定义。

• 决策：站在人生的岔路口，我清晰地看到眼前有很多条路。沉思良久，我选择了其中之一。
• 正误：我选了A，但到头来却发现，我应该选B。

为什么要强调“决策”和“正误”的定义呢？极端地说，我们的人生是一道又一道的选择题。你下一刻可以哭，也可以笑。你下一刻可以打开抖音，也可以打开王者荣耀。我们无时无刻不在作决策。如果我们对决策的标准宏大一些：选哪所初中；选哪所高中；高考填志愿；大一转专业；未来出国、保研、考研、考公、就业还是创业。在前文的定义下，人的决策不多，而且判断决策的正误很难。没有岔路口，某个行为算不上决策；未经过足够的思考，某个选择也算不上决策；先有决策，后有正误，而且正误成立的前提是“你较为准确地预见了其它选择的未来”。

• 错误的决策避无可避。初期，基于极低的认知水平和极差的信息素养（包括信息差），作出所谓“错误”的决策再正常不过。
• 决策的属性之一是“走完了这段路，才可能知道决策的正误”。比如，本科的一些课程，我只想考六十分，但怕挂科，所以稍微多浪费了一些时间复习。矛盾之处在于“在没考之前，我不可能知道考试水不水、有多水”。

2. Bayes' Theorem

本小节顺着《概率论与数理统计》Bayes' Theorem的视角继续解构决策的成败。

成功和失败都是一种信息。失败可以用于修正错误的认知。

• 在拥有结果（成败）这一信息B之前， $P(A)=P(A)$ 。
• 在拥有结果（成败）这一信息B之后， $P(A|B)=\frac{P(A\cap B)}{P(B)}$ 。

在形式化的层面上，结果的本质是一样的，即通过实践所产生的先验信息。参考神经网络的训练过程，神经网络才不会因为误差的大小黯然神伤。它只会无情地执行最优化过程。

0x06 迭代

这涉及工科生不一定学的《数值计算》。它融合了《微积分》的敛散性、《线性代数》的“数据结构”（向量和矩阵）和《概率论与数理统计》的统计规律性。因此，本节不展开《数值计算》的术语。以第一节的时间管理为例：

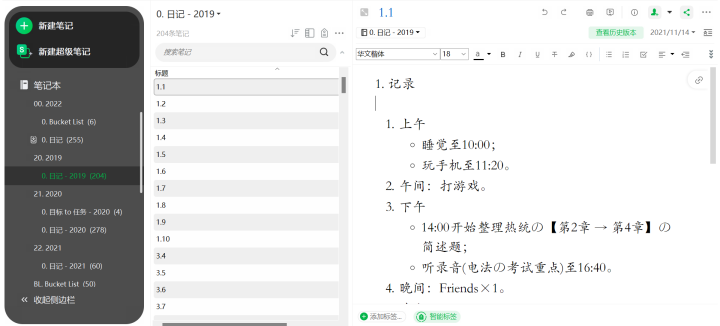
从这张图，你们可以得到哪些信息？

• 2019：又是一年新气象，心血来潮，写写日记吧！写了10天，烂尾了。
• 2020：多了笔记本《目标 to 任务》。
• 2021：只写了60篇日记，《目标 to 任务》没了。
• 2022：每天都写了日记，多了笔记本《Bucket List》。
• 2019-01-01：上午报废；下午低效地学了3h；晚上学了2.5h（效率一般）。

所谓的时间管理大师，不是一开始就是时间管理大师，而是：

• 毫无计划可言，粗略地记录当天干嘛了。
• 因为考试周，所以学了半天（否则可能一点也没学），但学习模式问题很大，有点拖延症加形式主义。
• 这甚至不是最初的版本，我2021年将所有日记的格式整改了一遍。早期日记的字体、章节、缩进、以及为了不断更的灌水等等，比上述版本更烂。

如果你想通过日记驱动自我管理，不妨从“记录”开始。单单记录，你就可以感受到自己荒废了多少光阴。

2019-01-01：第1篇日记

2019-03-04：第1篇考研日记

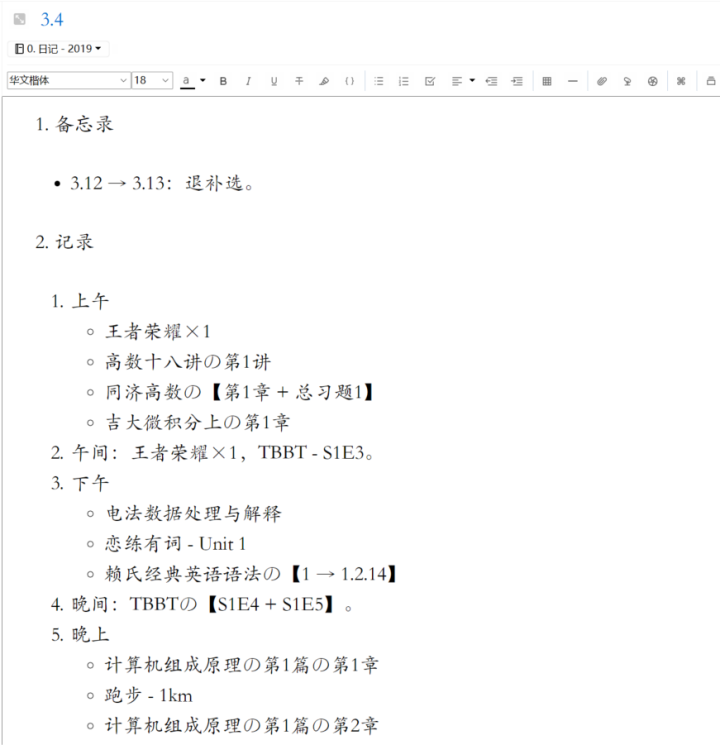
2019-05-01：奇怪的插曲

2019-06-20：出现了，计划！

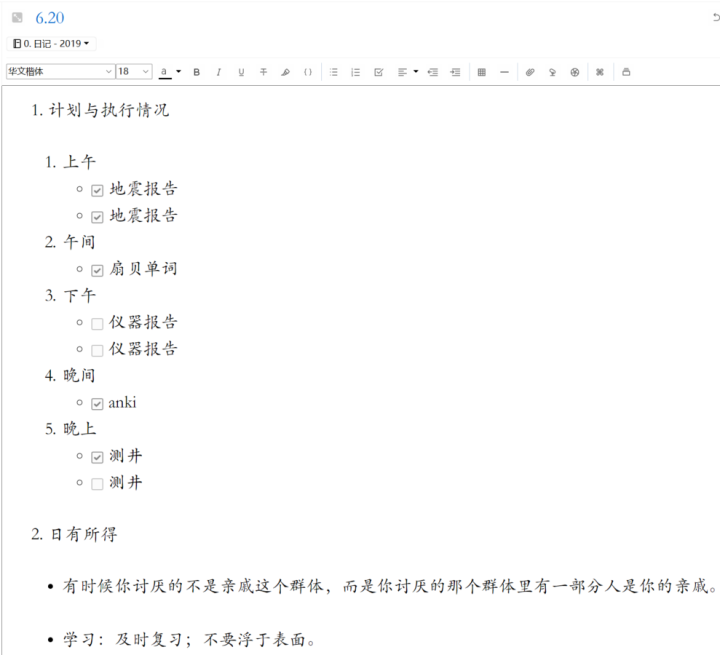
再看看考研二战期间的顶级生产力：

最后才是第一节的形态。

迭代的前提是“敛散性”。其核心要素是迭代法及其迭代步长。

0x07 求仁得仁

本文泛化了《下篇：自我教育/2 数学/1 凡人皆需数学》的第1节“引例：最高年薪”并详细地展开了《下篇：自我教育/2 数学/3 人生模型》的第3节“求仁得仁”。基于“目标 to 任务”的时间管理，我在“每个目标的各个周期”和“目标与目标的衔接”中使用了一些的数学定义和数学思想。“目标模型”从本质上是“做成一件事情”的抽象。

1. 可行性分析：事情能不能做成？内部条件和外部条件是否充分？
2. 决策：可以做成的事情很多，做哪些呢？
3. 计划：将大事拆解成小事，每天只需要搬砖就行了。
4. 成败：人不应该总是做胜券在握的事情，因为那样放弃了走出舒适区所遇到的可能性。既然如此，如何接纳失败，并从失败中获得成功的养料？
5. 迭代：如果以每个目标为一次完整的训练周期，如何将实践目标所得到的成长作用于下一个目标？

在以上“做成一件事情”的核心步骤中注入数学的力量，整个目标模型的归宿是“求仁得仁”。